Introduction
According to Zakaria (2020), teachers who put reflection into practice (i.e., reflecting on what they did in previous classes) teach better. That is, reflective practice in teaching is essential for the teacher to improve classroom instructions and then enhance student learning outcomes (Zakaria, 2020). In addition, as Mathematics, in its nature, serves as a link to other subjects, it is yet critical to developing well-rounded students if the classroom instructions are still critical without the reflection of the work done during the process of learning and teaching with the teacher as facilitator (Chapman, 2015; Drobnič Vidic, 2023; Kafata & Mbetwa, 2016; Visser et al., 2015).
Yet, Researchers in the Mathematics education area have endless concerns about how to fix Mathematics Teachers' knowledge specific to Mathematics teaching (Chapman, 2015). Mathematics performance can therefore be improved by applying the practice of reflection. The practice of reflection was found to be positive in improving productivity in health and education (Haghighat, 2020).
According to Yeasmin (2017), Mathematics is everywhere in other disciplines, including itself, health, and education. Henceforth, reflection practice is essential and beneficial for improving outcomes in Mathematics. It is, therefore, time to think of finding a 21st-century tool to help Mathematics teachers continuously teach constructively in classroom instruction. The 7E model approach is among the 21st-century approaches which build on constructivist principles and on other theories informing active participation in class (Eisenkraft , 2003).
There may be a theoretical gap in the literature, especially as not many tools have been developed to observe and reflect on 7E model-based mathematics lessons. Only tools to observe and teach mathematics and other trends, without emphasising reflecting on the lesson taught with the type of instructional model, were worked out in Rwanda and in other countries like Japan (Artzt et al., 2015; Ingram et al., 2018; Monaghan et al., 2016; Nkundabakura et al., 2023; Sakai et al., 2024). Indeed, no scholarly research would be conducted on any tool that combines Terry Borton’s model with the 7E framework. Consequently, a reflective framework is needed to help Mathematics teachers maintain constructive teaching practices.
Study Design
The design of this theoretical article is centred on its structure, which is how ideas, theories, and existing literature are used to develop the tools needed by this study. Therefore, it employed practical methods from the Terry Borton model of reflection (Borton, 1970) that were published in the book with the title “Reach, Touch and Teach”. The authors of this paper found this model to be one of the most straightforward models that can be used to adapt a tool to observe 7E model-based mathematics lessons and, consequently, produce a significant reflective tool to be used after class in the post-class observation discussion session.
The existing literature informing Terry Borton’s model, the 7E model framework and three theories, social constructivism, social learning and assimilation theories, were focused on. By analysing, synthesising, and interpreting them, this study produced meaningful tools for guiding good practice in motivating mathematics teachers to continually improve students’ outcomes in mathematics and maintain constructive classroom instructions. This study subsequently provided answers to its research questions.
Purpose
This study aimed to adapt Terry Borton’s reflective model to develop a tool for observing and analysing a 7E model-based Mathematics lesson, as well as a reflective tool to keep mathematics teachers updated on ways of producing good outcomes. It has two guiding questions, namely:
How can Terry Borton’s reflective model be adapted to produce tools for observing, analysing, and interpreting a 7E model-based Mathematics lesson?
How do the adapted Terry Borton’s reflective model tools help identify gaps in student engagement for future improvement of teaching and learning practices?
Models and Theoretical Framework
7E Model Approach
According to Eisenkraft (2003), supported by other researchers like Bertiliya et al. (2023), Bybee et al. (2006), Bybee ( 2014), Karaşah and Yaman (2017), and Khan et al. (2020), the 7E model approach is an active and learner-centred approach to teaching based on the 7E model and 21st-century active teaching and learning strategies. These strategies are among others listed according to their functions in class:
Pedagogy of play and problem-based learning, storytelling, context, discrepant event, inquiry-based learning strategies, simulation and gamification strategies for creating an active learning environment, reducing multitasking and taking a short break to promote focused attention among students (Havenga et al., 2023).
Flow charts, graphic organisers, demonstration, concept maps and Venn diagrams for promoting the connection of knowledge (Schwendimann, 2023).
Previewing Content and problem-solving strategies for helping students be able to organise their knowledge and then retain it (Marchant-Araya, 2024).
Ticketing strategies in different ways, and project-based learning for providing timely feedback in the next class (Bohara, 2024; Gök et al., 2020).
Formative assessment strategies for demanding quality in the class (Boström & Palm, 2023). Communication strategies for finding balance among students in class (Ball & Barzel, 2018).
ICT and computer-based interactive materials (such as animation, simulation, video, soft model) for enhancing interest and intrinsic motivation among 21st-century students in Mathematics classes (Asad et al., 2022; Boadu & Boateng, 2024).
Conventional Teaching Methods (CTM) are referred to as non-productive teaching methods compared to 21st-century strategies (Serbaya et al., 2024; Warner & Kaur, 2017). This study preferred the 7E model approach to be used in teaching mathematics, as it is only effective for achieving good outcomes when the strategies employed are innovative and 21st-century.
In the teaching and learning using the 7E model approach, active teaching and learning strategies are used through seven phases or steps: elicit, engage, explore, explain, elaborate, evaluate, and extend. Bybee (2014) when studying the applicability of the 7E model approach, the emphasis was only put on knowledge transfer, not on how the model can assist in academic concept knowledge retention and students’ interest in the subject content learned.
The 7E model approach is naturally rooted in constructivist principles (Eisenkraft, 2003), and it is also used in teaching and learning by referring to social learning theory to support interactions in class (Rumjaun & Narod, 2020). It falls into an instructional model featuring knowledge application and skills development, which is the primary purpose of the competence-based curriculum (CBC), that has been in use in basic education since 2015 in the Republic of Rwanda (Rwanda Education Board., 2015) and since 2017 in the Republic of Kenya (Kenya Institute of Curriculum Development, 2017).
A solid background in algebra, often regarded as the language of mathematics, has a positive impact on students' performance in various disciplines, including mathematics itself (Grønmo, 2018). This study, which produces 7E model-based mathematics teaching and learning guided tools to facilitate professional development among Mathematics teachers in their community of practice, is relevant and makes a significant contribution to the implementation of the Competency-Based Curriculum (CBC).
Terry Borton’s Reflective Model
Terry Borton’s reflective model is one of the simple models of reflection developed by Terry Borton, an American school teacher, in 1970. Its methods are based on three prompt expressions “What?” “So what?” and “Now what?”. These prompt expressions were found to be used as the reflective prompt questions for developing teaching materials. These methods were first published in the 1970 book entitled “Reach, Touch and Teach” (Borton, 1970).
These three prompt expressions were simplified to help people reflect on their experiences and gain a deeper understanding of what happened, why it happened, and what can be done to improve the situation next time. As shown by the empirical assessment by Raghupathi and Raghupathi (2020), education impacts health. Therefore, reflecting on health is indirectly related to reflecting on education.
In addition, the practice of reflection was also found to improve productivity in health and outcomes in education positively (Haghighat, 2020). Therefore, in teaching and learning, we can refer to the work done by professors Rolfe et al. (2001) and endorsed by Driscoll (2006) when adapting a model in clinical practice, and taking it as a model for reflection. The model is written in 7 stages, which are almost similar to the 7 phases of the 7E learning model (Eisenkraft, 2003).
In fact, they described the three Borton questions to guide nursing and healthcare practitioners in their work. Terry Borton’s work also inspired those professors in 1970, when the three prompt expression questions were discovered in education. Theories versus the Use of the 7E Model and Terry Borton’s Model
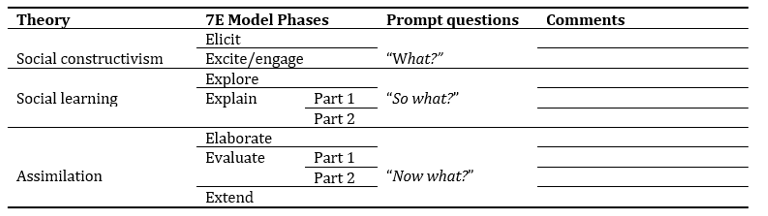
To adapt Terry Borton’s reflection model, this study was guided by three main theories by experts in the field of research study (Kivunja, 2018). These are Lev Vygotsky’s social constructivism theory [In this theory, the views of Jean Piaget and Lev Vygotsky were highlighted by Devi (2019) and MacBlain (2018)], social learning theory developed by Bandura (1977) and highlighted by Rumjaun and Narod (2020), and then the theory of assimilation in meaningful learning and retention processes (Ausubel, 2000).
Social Constructivism Theory
According to the social constructivism theory, the goal of learning is not to store a large mass (i.e., piles) of information in a student's head, but to engage the student’s mind by constructing practical, powerful and meaningful concepts (Devi, 2019). In order to respect how people would effectively learn constructively, Eisenkraft (2003) confirmed a new learning cycle instructional model, called the 7E model. This model was developed based on the amendments made to the highly successful BSCS (Biological Sciences Curriculum Study) 5E learning cycle instructional model. The BSCS 5E instructional model was created in 1987 by Bybee and his team (Joswick & Hulings, 2024), and personally reflected on it to make it more effective (Bybee, 2014; Bybee et al., 2006).
As far as the social constructivist theory is concerned, the 7E instructional model strategies are used to emphasise learning transfer by recognising the value and importance of eliciting prior knowledge and sharing objectives with learners before actual teaching takes place. The sharing objectives is done when learners, based on their prior knowledge, raise their questions on a used problem-based situation material (either a story, a context, a discrepant event, demonstration, animation, video, or a model) by the teacher to promote curiosity among students (Asad et al., 2022; Boadu & Boateng, 2024; Havenga et al., 2023; Schwendimann, 2023). How good students are excited by the good use of suitable material by the teacher, they ask questions. From those questions, the teacher helps students identify their key points and ultimately helps them formulate a single question based on them. The formulated question, similar to what is written in the developed lesson plan and formulated from instructional objectives, is called the “key question”. It guides the achievement of lesson objectives throughout all lesson activities.
Therefore, the two key actions (eliciting or detecting prior knowledge through brainstorming or pretesting and sharing objectives with learners by formulating a key question) are guided by constructivist theory, which informs the study about two phases of the 7E instructional model: “Elicit” and “Engage”.
Based on this theory and Terry Borton’s model adapted in the 7E instructional model framework, social constructivism theory informs the ‘What?’ prompt question by emphasising prior knowledge elicitation and sharing lesson objectives. Consequently, analysing the prompt question “What?” together with Driscoll (2006) and Rolfe et al. (2001)’ descriptors (see Table 2). This study retains a teaching and learning prompt question descriptor to be “what happened”. This will be specified by questions like “What was the role of the teacher and students? What did they do?, and What did the students do?”.
Social Learning Theory
Bandura's social learning theorysupports using the 7E model strategies to emphasise interaction in the Mathematics class. This idea, as proposed by Bandura (1977), and highlighted by Rumjaun and Narod (2020), emphasises that students learn from interacting with others in a social context, such as in inquiry groups within a shared classroom. This aligns with the 7E instructional model's “Explore” phase, where students primarily engage in practical work in a social and inquiry-based manner, typically in groups.
It is true, as it is supported by Ahn et al. (2020); when students observe others’ behaviour, they learn from one another, and the teacher rewards their learned experiences when they “present/show what they have found from their group” activities and then are given “constructive feedback or supplements by the teacher”. That is, the two successive actions (“presentation of findings by students” and “constructive feedback by the teacher” in supplementing the work of students to clarify the lesson concepts) informed by the social learning theory and also guarantee one phase from 7E instructional model which is clearly divided into two parts: “Explain part one” (which is about the “presentation of findings by students”) and the “Explain part two” (which is about the “constructive feedback by the teacher”).
Henceforth, social learning theory supports the ‘So What?’ prompt question through group-based exploration. When students are given a group activity, they try it to see what they can learn from it. Hence, analysing the prompt question “Sow What” together with Driscoll (2006) and Rolfe et al. (2001)’ descriptors (see Table 2), we retain a teaching and learning prompt question descriptor to be “What can the teacher learn from what happened?”. This will be specified by questions like “What was so important in the experience? Why did it happen that way?, and What did the teacher learn?”.
Assimilation Theory
By the assimilation theory, Ausubel’s assimilation theory of learning in different years (1963, 1968 & 1978) describes the process through which a student engages or a teacher finds a way of engaging them for meaningful learning through steps that end by helping them to retain what is learnt/concept retention for a long time (Ausubel, 2000). That is a psychological mechanism stipulating that large amounts and/or quantities of subject-content knowledge are retained once learned through a cognitive or a known active learning and teaching model. As a result, the learned content will be extended over time to learn other subsequent knowledge (Ausubel, 2000).
Therefore, the teaching and learning through the 7E model approach requires innovative strategies, and is done through structured steps or phases, among them, some are meant for assessing in a structured way to avoid discrepancies within the steps’ components (Eisenkraft , 2003). The assimilation theory, then, informs the 7E model through three actions. First action in assessing whether students can “apply the acquired knowledge” in another situation or real life, second action in verifying if the “lesson has been effective or took place”, and third action in determining if students can “utilise the acquired knowledge to acquire other meaningful knowledge”. It therefore guarantees the existence of the last three phases of the 7E instructional model, which are respectively “elaborate”, “evaluate” and “extend”.
The assimilation theory and 7E instructional model agree, as the above three actions and their corresponding phases are effectively applied using innovative strategies for effective 7E model-based mathematics lesson delivery. That is, innovatively, for the elaborate phase, an elaborate or application activity is given as a challenging situation to be addressed by applying the learnt knowledge. In Mathematics, the activity is given in a procedural way different from what was used in previous phases of the lesson, or an experiment to apply the learnt knowledge. The “evaluate” phase is also used when students are given the final lesson assessment questions. Those questions are only meant to check whether students have retained the learnt competence, which can justify why the lesson took place. Failing those questions means that no lesson occurred; that is why, in Mathematics, before giving such kinds of questions, as referred to in the assimilation theory informing assessment, the teacher prompts learners to recall the key lesson points, which, once remembered, are the ones used to solve the assessment questions. The “evaluate” phase is therefore conducted in two parts: the first part involves “provision of key lesson points or exit ticket”, and the second part is the “final lesson assessment”, which includes direct questions to check the achievement of lesson objectives. Finally, using innovative teaching and learning strategies that draw on assimilation theory for a 7E model-based mathematics lesson, the “extend” phase of the 7E instructional model is approached in an inquiry-based manner. Students are assigned a home activity, commonly referred to as “homework,” to continue learning, deepen their knowledge, and acquire additional knowledge and skills (Olufemi, 2014). The activity can be either an individual research-based activity or a real-life project.
Furthermore, the assimilation theory supports the “Now What?” prompt question from Terry Borton’s model by applying the gained academic concept, checking whether learning has taken place, and extending the learnt competence through individual homework assignments at the end of the lesson. Consequently, analysing the prompt question “Now what?” together with Driscoll (2006) and Rolfe et al. (2001)’ descriptors (see Table 2), we retain a teaching and learning prompt question descriptor to be “how will the teacher use what was learnt from what happened?” or, “how will the teacher work to improve teaching and learning”. This will be specified by questions like: What does the teacher change for better practice? What will be his/her new actions?, and what will be the results of applying new actions?
By combining the three theories employed in this study and models (the 7E instructional model and Terry Borton's Reflective model), we obtained an “Analysing Framework for a 7E model-based Mathematics lesson” (see Table 1), which serves as a non-detailed classroom observation tool (a detailed version is provided in Appendix A).
Table 1. Analysing Framework for a 7E Model-based Mathematics lesson
Gaps
There would be a research gap in the area of Terry Borton’s model versus the 7E model framework and mathematics teaching and learning. Not much information from scholarly studies in the same area has been conducted in Rwanda and outside, especially as Eisenkraft (2003) confirmed the extension of the 5E model to the 7E model framework, which was, afterword, verified and endorsed by Bybee et al. (2006), Bybee (2014) and Eisenkraft (2003) to be a science lesson model framework. Tools emanating from this study are applicable in schools by teachers. These teachers may not be competent in teaching mathematics using the 7E model approach, and there may be a lack of classroom observations for professional development culture among teachers at their school. Training on the guided tools produced by this study, which can be costly, is mandatory to disseminate the findings.
| Prompt Question | Descriptors by Rolfe et al. (2001) | Descriptors by Driscoll (2006) | Retained/concise descriptors in education matters |
| WHAT? | what is the difficulty/ the reason for being stuck/the reason for feeling bad/the reason we do not get on/the problem? what was my fundamental role in the situation? what did I try to achieve? what necessary actions did I take? what was the answer of others? what were the direct consequences on myself? For the student? Myself? On others? what feelings does it evoke in me? In the student? In others? what was bad/good about the experience? | what happened today?what was my initial reaction?what were the reactions of others?what was the issue or the problem?what was challenging or good about that experience?what feelings did it bring up for me?what did I expect? | What happened?I describe my experiences and actions, as well as those of students.what was my active role?what did students do?what did others do? |
| SO WHAT? | so what does this tell me/teach me/imply/mean about me/mean about my class/mean about others/about our relationship/about my patient’s care/is the model of care I am using/my attitudes/is my patient’s attitudes? so what went through my mind when I acted? so what did I base my actions on? so what can I bring to the situation as other knowledge?so what should/could I have done to make the thing better?so what is my new understanding of the situation? so what big issues arise from the situation? | so what does this teach me about myself?so what does this teach me about my skills or knowledge to respond to the situation and to others?so, what scholarship/literature/theories/ standards explain or align with this experience?so what must have been done differently to make it better? | What can I learn from what happened?I have to analyse and reflect on the experience I had in the class:What was so important about the experience in class? Why did it happen that way?What did I learn? |
| NOW WHAT? | now what do I need to do to make things better/stop being stuck/do I need to improve my teaching/do I need to resolve the situation/do I need to feel better/do I need to get on better? now what broader issues need to be considered if this action is to be successful? now what might be the consequences of this action? | now what do I know about myself that will inform my career?now what do I know about myself that can shape how I perceive my strengths and interests?now what must I do to improve my knowledge/behaviour/skills for a better future?now what steps will I take to advance my career?now what steps will I use to find other helpful people for me? | How will the teacher work to improve teaching and learning?It means I draw conclusions after reflecting on my experience: What do I change to make such an experience happen better next time? What will be my new actions?What will be the positive impact of my new actions once applied? |
Conclusions
Analysis
After exploring, synthesising and combining Terry Borton’s model with 7E model framework, and trying to interpret the results by the help of the existing related literature and theories, the study put out an Adapted Terry Borton’s Reflective Model Lesson Observation Tool called “Classroom Observation-Guided Tool” (see Table 1 as detailed in Appendix A). After a pilot application on eight Mathematics lessons, this tool was refined to look at how it is presented in this article. These Mathematics lessons of four teachers were observed from four schools chosen purposively based on their locations: two rural and two urban schools, as the two constraints identified affected students' performance, as in the report by National Examination and School Inspection Authority (2023).
The school’s equivalence also influenced school choice: those with relatively good standards in terms of infrastructure, teaching resources, physical availability of ICT and computer-based resources, presence of qualified and experienced Mathematics teachers, experienced school head teachers, and their deputies. The choice of these constraints was motivated by the fact that the 7E model strategies require both hard and soft teaching resources, as well as competent and trained teachers, to be effectively implemented through the model. Also, the choice was affected by school leadership, as good leadership practice was confirmed to affect the performance of students in Rwanda (Ndagijimana & Uwimbabazi, 2025) and outside Rwanda, like in South Africa (Memela & Ramrathan, 2022).
In addition to the acquired background, the study's first author trained these four teachers in teaching mathematics using the 7E model approach. They were then observed teaching algebra topics by applying what they had learned from the training. The choice of algebra topics was motivated by the fact that students with a good algebra background perform well in Mathematics and other subjects (Juraev & Bozorov, 2024; Niringiyimana & Maniraho, 2023). Indeed, algebra plays an important role in mathematics as it is taken as its language (Grønmo, 2018).
They further underwent a post-lesson observation discussion, and from there, they were advised to strive to find more suitable resources to teach mathematics lessons effectively through the 7E model framework. Every teacher was visited twice in the intact classroom.
This study also put out the second tool, which is the post-lesson observation discussion checklist tool called “Post-Lesson Discussion Guided Tool” (as detailed in Appendix B). It was found by synthesising the Appendix A and referring to innovative aspects identified from eight classes, as well as from the discussions held between the first and second classroom observations, and after second classroom observations, to develop an informative tool that can help teachers identify gaps in student engagement, enabling them to improve their next teaching and learning practices.
Discussion
Meaning of Findings vis-à-vis Research Questions:
This study had two objectives: How can Terry Borton’s reflective model be adapted to produce tools for observing, analysing, and interpreting a 7E model-based Mathematics lesson? How do the adapted Terry Borton’s reflective model tools help identify gaps in student engagement for future improvement of teaching and learning practices?
The first question was answered by exploring, analysing, interpreting and synthesising three existing theories (social constructivism, social learning, and assimilation), prompt descriptors (see Table 2) and then adapting Terry Borton’s reflective model by combining it with 7E model framework for better understanding the 21st-century Mathematics teaching and learning practices for good outcomes. The found observation tool (see Table 1 as detailed in Appendix A) can serve as a tool for observing a 7E model-based Mathematics lesson. It therefore answers the first part of the first question.
In addition, the remaining part of the first question and the second question were also answered after finding the post-lessonobservation discussion checklist tool called “Post-Lesson Discussion Guided Tool” (see Appendix B). This was discovered by processing a pilot application of the classroom observation-guided tool on 7E model-based Mathematics lessons, considering the innovative aspects found in eight observed lessons, and through post-lesson observation discussions conducted after all eight observations (answer to the second question).
Therefore, by using the “Post-Lesson Discussion Guided Tool” toanalyse and interpret the conducted 7E model-based Mathematics lesson, in post-lesson discussion sessions, gaps in students' engagement will be identified, and in turn, the concerned teacher will take their “Now what?” for their next Mathematics lessons' improvement (answer to the second part of first question).
The Practical Use of the Produced Tools, obtained by Adapting Terry Borton’s Model:
In a community of practice for professional development among Mathematics teachers in a school, the adapted 7E model-based Mathematics lesson observation tool called “Classroom Observation-Guided Tool” (see Table 1 as detailed in Appendix A), as a version of teaching practice model for good outcomes, would require teaching focusing on specific phases of the 7E model. The observer is asked to complete the tool in class.
Before the real post-lesson discussion takes place, a copy of the “Post-Lesson Discussion Guided Tool” is given to the observed teacher so that they can fill it out before meeting the teacher who observed the lesson in the discussion session. In a real post-lesson discussion session, the discussion primarily leads to the construction of “now what?” as the final phase of the what model.
When entering the post-lesson observation discussion session, the observed teacher starts their turn by sharing their insights on what went well, what did not, and what needs improvement in future learning and teaching practices. The teacher who observed the lesson in their turn, the “now what?” phase of “what model” is the main target to be emphasised with their directives. The discussion is based on the filled classroom observation-guided tool in class by the observer and the filled reflection tool out of class by the observed teacher. The observer completes the reflection tool live during the discussion session, using the outcome of the discussion.
The observed teacher, using comments’ place (see it on Appendix B), takes notes of the phases of the 7E instructional model that were not well used and why during class and should critically plan for necessary improvements that fit their next learning and teaching practices. All parties leave each other after agreeing in writing and signing the reflection tool, outlining the way forward.
Limitations and Recommendations
As a limitation, both guided tools have been newly developed; they may not be easily applied by people who are not trained to use them. Training on them is needed. It is therefore recommended that countries where CBC is being used utilise these two guided tools, as outlined in this article, in teacher training institutions to inform pre-service teachers about them. Otherwise, training in-service teachers may take a long time and be even more expensive; it can be considered a second option.
Other researchers can study the applicability of 21st-century observation and reflection-guided tools to other subjects, not only Mathematics, exploring their long-term impact on teacher professional development to improve overall student achievement in all disciplines within a school.
Acknowledgement
We, the authors, would like to thank the University of Rwanda College of Education (UR-CE) for admitting the first author of this article to PhD studies and for providing the necessary help when appointing the second and third authors as co-supervisors, as well as for the hospitality during the preparation of this article.
Conflict of Interest
Authors declare no competing interests.
Funding
So far, the study has been conducted with the authors’ self-funding, with all research expenses covered by the researchers themselves.
Generative AI Statement
The authors confirm our full responsibility for the content of this article. In fact, we used the Grammarly AI tool to proofread the manuscript for language accuracy. After using it, we reviewed our work and verified the final version before submitting it to IJEM.
Authorship Contribution Statement
Habimana: Drafting and writing manuscript: writing the introductory text, methodology development, tools design, results and discussion. Bizimana: Writing the contribution to literature, results and discussion and text proofreading, whole work supervision. Mairano: Development of the conclusion and text proofreading, whole work supervision.
Appendices
Appendix A: Classroom Observation-Guided Tool
Observation’s Identification Part:
Specified Grade: …………………………
Number of registered students ………….… present: ……… (……..Female and ………….. Male)
Number of students with Special Educational Needs (SEN): ……. …. Specify cases: ……………………………………
…………………………………………………………………………………………………………………………………..
Lesson title: …………….
Lesson objectives: (Tick or cross on ABCD essential components): A…….…… B……….… C…….……. D………….
Date of the observation: ………………. Number of periods for the whole lesson: …… Duration: from … to …
Name of the Mathematics teacher: …………………….
Table 3. 7E model-based Mathematics Lesson Observation Tool as adapted by this study from Terry Borton’s Reflective Model
| Borton’s Reflective Model with Main Steps’ Descriptors | Reflection Notes on Phases of the 7E Instructional Model/Elicit | 7E Instructional Model Phases in Relation to the Main Steps’ DescriptorsElicit and Excite/Engage in relation to WHAT?’s descriptorsWHAT? is like “What happened?” | Comments by the Teacher Observer |
| WHAT? What happened?I describe my experiences and actions, as well as those of students.what was my active role?what did students do?what did others do? | By actualizing the first step, WHAT? For the current learning and teaching process, the elicit and excite/engage phases are where students confirm their prior knowledge related to the concept planned to be taught. Elicit by detecting how confident students are vis-à-vis the prerequisite knowledge for the current lesson concepts (teacher checks from the previous curricula if, among previous lessons, even in previous years, there was a certain lesson with concepts connected to the current lesson as its prerequisite). Excite/engage by sharing lesson objectives with learners. The teacher using problem-based situation material creates curiosity in learners so that they raise questions, and the identified key points from those questions are used to formulate a key question similar to what was developed, emanating from lesson objectives. The raising questions method is often used. | 1st as elicit or detecting prior knowledge: “What was the role of teachers and students?”Like initially helped by teacher, what did you (student) learn about … (three dots can be replaced by a concept or a mathematics expression that teacher has qualified prerequisite to the current lesson concepts)NB: During the development of the lesson plan, the teacher has to consider why the current lesson occurs at that time after others. I.e., among the things/concepts learnt so far, it is not possible to miss some related (as prior knowledge) to the current lesson concepts, prerequisite. | |
| 2nd as excite/engaging learners to formulate key question:“What did teacher and students do, what did others do?”Like what student can do to be able to understand either he/she is doing(realistic situation or context, etc..) , or what actual teacher does(demonstration, discrepant event etc..) or what others did (animation, etc…). NB: In every case, a problem-based situation material, to create curiosity among students, is used to lead to the formulation of key question | |||
| Explore and Explain (part 1&2)By actualizing 2nd step, SO WHAT?, for the current learning and teaching process, the explore and explain phases are related to SO WHAT?. | Explore and Explain in relation to SO WHAT?’s descriptorsSO WHAT? Is like “what can the teacher learn from what happened?” | ||
| SO WHAT? What can I learn from what happened?I have to analyse and reflect on the experience I had in the class:What was so important about the experience in class? Why did it happen that way?What did I learn? | In Explore, students mainly perform practical works in a social and inquiry mode, just in groups. It means that when students observe others’ behaviour, they learn from one another. | 3rd as explore: “What was so important about this experience?” By actualizing the “so what?” step, its first descriptor informs explore phase. Students should be given an inquiry activity that helps them explore what is happening and why it is happening in that way. Mainly, that activity is an experiment, or a well-sequenced exercise written in more than one step that finally leads to the lesson concept or ends/last step with something to conflict again students by creating an extra question. | |
| Explain part 1Students present their findings from their social and inquiry group activities | 4th as explain part 1: “Why did it happen that way?”Still, by actualizing “so what?” step, through its second descriptor, it informs explain part 1. The teacher needs to confirm whether what they saw in different groups when students were working in their groups is what students accepted as their knowledge. Students are given time to present their findings, showing what they have so far put into their heads in terms of knowledge related to or leading to the lesson concepts. They present in terms of defending their findings, to confirm the basis on which the teacher will use to share, hand out, or teach students, ensuring that students have the information they have so far learnt. Alternatively, the teacher learns how to help students learn better. The teacher has to only point out weak points from what learners are presenting, but they don’t have to stop any presenter; all presentation outputs are important and therefore needed. | ||
| Explain part 2Students receive feedback to confirm what they have presented as new knowledge, informing the lesson concept, or to supplement what has been presented to make the learning effective. The teacher is the key in this part 2 of the explain phase. | 5th as explain part 2: “What did the teacher learn?”By actualizing the “so what?” step, its third descriptor informs explain part 2. In order for the teacher to complete or supplement on what he/she put down while students were presenting (i.e., what he/she have learnt from presentation), they take time to explain, to give examples, to clarify what were presented, to clarify the lesson concepts, to perform examples/exercises as to show the good way of working as someone who acquired that lesson concepts. In short, after the learners’ presentation, the teacher, using what he/she has developed before entering class, harmonizes/teaches/explains well/gives examples/reminds applications/gives feedback/completes what students have presented (explain part 2). All these are for the purpose of making the lesson concepts known and understood well. | ||
| Elaborate, Extend and evaluateBy actualizing 3rd step, NOW WHAT?, for the current learning and teaching process, the Elaborate, Extend and evaluate phases are related to NOW WHAT? | Elaborate, Evaluate and Extendin relation to NOW WHAT?’s descriptorsNOW WHAT? Is like “how will the teacher work to improve teaching and learning?” | ||
| NOW WHAT? How will the teacher work to improve teaching and learning?It means I draw conclusions after reflecting on my experience: What do I change to make such an experience happen better next time? What will be my new actions?What will be the positive impact of my new actions once applied? | In the elaborate phase, the teacher challenges students through new experiences, and the students develop deeper and broader understanding, more information, and adequate skills. In short, in elaborate phase, students apply their gained knowledge and understanding of the studied concepts by conducting/performing additional activities. Activities done in a procedural way different from the ones used in previous phase activities. | 6th as elaborate: “What do I change to make this experience better?” Or “what does the teacher change for better practice?” By actualizing the now what step, its first descriptor informs elaborate phase. Teacher has to check if really students have understood and acquired the lesson concepts through strategies used in previous phases or not. If he/she finds positive or negative sign, he/she keep using or change respectively strategies. Specifically, students should be exposed in new situations so that once they can be able to adapt the learnt concepts in that situation, it means they are able to apply what they have learnt, or they are able to make the change on the obtained experience to make it better or to use it in daily life. In Mathematics, this is done when students are given an exercise/activity in a different way from how the exercises/activities have been given in previous phases. This means that if the student is able to solve/work on that procedural exercise/activity, it means he/she has sharpened his/her related skills, and he/she is also able to use the newly acquired concepts and competencies in his/her real life. | |
| Evaluate part 1&2, teachers assess if students are going to leave class with important points from the lesson. They also check if the lesson has taken place or if objectives have been achieved (i.e measuring the achievement of lesson objectives or measuring the student's grasp of the lesson concepts and competencies they were expected to acquire over the lesson time) after they have shown engagement in the lesson learning process. | 7th as evaluate phase part 1&2: “What will be his/her new action?” Or simply, “What will be the consequences of my new actions?” By actualizing the now what step, its second descriptor informs elaborate phase (part 1: provision of key lesson points or exit ticket & part 2: final lesson assessment). In fact, to assess the consequences of the strategies used in previous phases, it is first necessary to verify whether students are leaving class with the key lesson points in mind, and second, to determine whether the lesson objectives have been achieved or not. The order in which to start depends on the students' mood. If the teacher judges that students are still in the lesson mood, they can start with assessment and then key lesson points; otherwise, they start with the provision of key lesson points. Specifically, in the normal way, detecting the exit ticket, the teacher uses prompt questions to facilitate learners' say about them. For the assessment, the teacher should have developed questions, such as exercises in mathematics (in the form of quizzes, tests, observations, discussions, reflections, etc.), in advance so that students are given tasks that utilise the action points/key lesson points provided in the exit ticket phase. | ||
| Extend phase. The students are given homework in order to extend their conceptual understanding and skills when using them for their individual research or in performing real-life projects. | 8th as extend phase: “What will be the results of applying new acquired actions?”Still, by actualizing the “now what?” step, its third descriptor informs the extend phase as the last phase in the 7E model approach. It comes at the end, or it is the one that is long among others. Therefore, it also requires the use of time after class. Teachers facilitate this phase by giving activities to students to be done at their homes, obviously individually, through what is commonly called “Homework”. The homework can be of a short time, when it is an activity that requires students to go through another experience, using the acquired concepts from today’s lesson, to recognise further knowledge and concepts before reaching the answer to the given activity. That is, the activity should be an inquiry-based activity to perform an inquiry-based experiment. The homework can also be of a long time, when students are asked to perform a project, and after a certain time, they will present the results by showing the additional knowledge and concepts learnt in the process of performing the activity and the product reached on. |
Appendix B: Post-Lesson Discussion Guided Tool
Reflection’s Identification Part:
Specified grade: …………………………
Number of students in class: ………… (………Female and ……… Male)
Number of students with special educational needs (SEN): … Specify cases: …………………………………………………………………………………………….
Lesson title: …………………….….
Number of periods used in class: ……... Date of the observation: ……………,
Date and duration of discussion: ……….… from…….…… to ………
Name of the Mathematics teacher: ……….….
Instructions:
Put a tick (✓) in the cell of “Yes” or “No” to assert whether what you have planned to do for an effective practical class happened or not. Provide informative comments, as required, in the explanations section.
Table 4. Reflective Tool for Post-Lesson Observation Discussion as produced by this study
| SN | Question/Item | Yes | No | Explanations |
| 1 | Did the teacher clearly help students to recall the known concepts related to today’s lesson? If so, which materials were used to do so? List them. | |||
| 2 | Did the teacher clearly help students to share lesson objectives? If yes, which strategy and materials were used to do so? List them. | |||
| 3 | Were students working collaboratively on a clear and informative activity in their groups, discussing by respecting each other’s ideas and contributions, using problem-solving together, and/or any other non-zero inquiry-based method? What methods and materials were used? List them | |||
| 4 | Did the teacher act as a facilitator, clarifying instructions to every learner and guiding students during different phases of the 7Es rather than providing direct answers using the Tennis methods? What are the techniques and materials used? List them in the explanation place. | |||
| 5 | Were students actively contributing ideas by presenting findings from their group activities, supplemented by the teacher to understand the lesson concepts, and then applying them using interactive or non-interactive materials? What materials and methods were used for that? List them. | |||
| 6 | Did the teacher provide relevant resources such as books, subject syllabi, online material, tools to use as interactive and/or manipulative materials, and ICT and computer-based interactive materials to support the teaching process? If yes, provide them in an explanation place. | |||
| 7 | Were students effectively utilising the provided resources (materials) to enhance their understanding of mathematics lesson concepts and their competence achievements? Explain. | |||
| 8 | Were there opportunities for students to reflect on their progress and then be able to apply the concepts learned outside the class through a straightforward activity? What methods and materials were used? | |||
| 9 | Did students work on an activity to apply the learned points, which allowed the teacher to measure the achievement of lesson objectives? What methods and materials were used? | |||
| 10 | Did the teacher help the learners say what they would leave class with and allow them to continue trying those learned points at home? What methods and materials were used? | |||
| 11 | Were all seven phases of the 7E model used during the lesson? If not, list what was not used, and the teacher say why they did not use them. | |||
| 12 | Was there a clear contribution of the 7E model approach to support the current country curriculum implementation compared to how CTM did? If no, explain; if yes, list the contribution in the explanation section. Provide at least three clear contributions of the approach used. |
General Comment by the Observed Mathematics Teacher:
Mathematics teacher (a place for providing any other points you can share, either what went well or not, and the general appreciation of the 7E model strategies in teaching Mathematics vis-à-vis CTM):
Your appreciation of the 7E model approach with CTM: ………………………………………………………………………………………
………………………………………………………………………………………
What went well: ………………………………………………………………………………………
………………………………………………………………………………………
If you can be given another chance to repeat the same lesson, what can you improve on? As you will teach other Mathematics lessons next time, what is your “now-what?” decision? ………………………………………………………………………………………
………………………………………………………………………………………
General Comment by the Observer:
With respect to what model, considering your discussion and the completed in-class lesson and after-class guided tools, especially the “now-what?” descriptor, what advice would you give the mathematics teacher to improve mathematics lessons for next time? ………………………………………………………………………………………
………………………………………………………………………………………
Mathematics teacher’s signature and date: ………………………………………….
Observers’ names, signature and date: ………………………………………………

